ベクトル 平行 条件
中学のときに習う中点連結定理を、ベクトルの世界で考えてみましょう。 三角形 ABC があって、辺 AB, AC の中点を、それぞれ M, N とおきます。 このとき、 MN は BC と平行で、長さが $\dfrac{1}{2}$ になる、というのが、中点連結定理の内容です。.

ベクトル 平行 条件. 逆格子ベクトル>> 「逆格子ベクトル」を用いると、結晶中の平行な原子面の組をまとめて表すことができる。 逆格子ベクトルの基底定義は下のようなもの(およびその循環式)で、 それぞれに整数の組(h、k、l)をかけたベクトルGはある原子面に垂直な. ベクトルの平行条件 (注) $\vec{0}$ でない2 つのベクトル$\vec{a}$ と$\vec{b}$ の向きが同じか,または反対であるとき,$\vec{a}$ と$\vec{b}$ は 平行 であるといい,$\boldsymbol{\vec{a} \parallel \vec{b}}$ と表す.. ベクトルの平行条件 2つのベクトル , について と が平行( ) となるための必要十分条件は となる実数 が存在すること ( となる実数 が存在することと言っても同じ).
さらに,ベクトル同士の和やk 倍は,成分ごとの和やk 倍になり,数ベクト ルとしての和やk 倍と一致する.すなわち,幾何ベクトルが数ベクトルで表 される. 共線条件 相異なる2点A,B を考え,位置ベクトルをa, b とする.点P(位置ベ. 4.2 2次元ベクトルの内積の計算例(2) 4.3 3次元ベクトルの内積の計算例;. 内積の平行条件の証明で (aベクトル・bベクトル)=|aベクトル|^2|bベクトル|^2を成分で表して証明するとあったのですが、やり方が分かりません(>人<;)教えて下さい。 あの、(aベクトル・bベクトル)^2ではないですか?成分aベクトル=(ax,ay),bべクトル=bx,by)とすると、(aベクトル・bベクトル)^2=(ax.
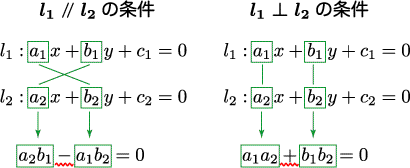
2直線 l_1,\,l_2 が \begin{cases} l_1:ax_1+by_1+c_1=0\\ l_2:ax_2+by_2+c_2=0 \end{cases} であるとします。それぞれの法線ベクトル \bm n_1. 耕一 平行ということは方向が同じで大きさは違ってもよいということなので, 0で. ベクトルの平行条件, である二つのベクトルに対し、 となる実数 が存在すること。,.
平面上の直線(その一) 上: 平面上の直線 前: 平面上の直線. 証明 はじめに 3次元ベクトル空間の任意のベクトルは、 3つの線形独立なベクトルによる線形結合によって表すことができる (「次元と同じ数だけある線形独立なベクトルは基底になる」を参考) 。 従って、 $0$ でない2つの線形独立なベクトル $\mathbf{a}$, $\mathbf{b}$ とそれらの間の外積 $\mathbf{a. 座標空間での直線と平面 平面上の直線 二つのベクトルの平行条件 南海 最初は,零ベクトルでない二つのベクトル と が平行である条件から考えよう..
前回 https://goo.gl/ghtH8T 次回 https://goo.gl/IHSl5l 動画のプリント(19ch) http://www.19ch.tv/ サブチャンネル とある男. 共線条件とは、三点が一直線上に存在するときに成立する条件の事で、 例えば点bが直線ac上にある時、 ab=kac (kは実数) の様に始点(ここではa)を揃えると、 abベクトルはacベクトルのk倍という式が成立します。これがベクトルでの共線条件です。. ベクトル G-1-1 ベクトルの加法の基本法則 任意のベクトルa, b, c について, ① 交換法則 a+b = b+a ② 結合法則 (a+b)+c = a+(b +c) ③ 零ベクトルの性質 a+0 = 0+a = a ④ 逆ベクトルの性質 a+(−a)=0,(−a)+a = 0 G-1-2 ベクトルの平行条件.
Try IT(トライイット)のベクトルの平行条件の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の. 空間ベクトルの平行条件$a_xb_y = a_yb_x$かつ$a_yb_z = a_zb_y$ つまり \begin{eqnarray} \left\{ \begin{array}{l} 2 \cdot 2 = (−1) \cdot (z −1) \\ −1 \cdot (z + 1) = 5 \cdot 2 \\ \end{array} \right. ベクトルの平行条件 \( \vec{ a } \neq \vec{ 0 } \),\( \vec{ b } \neq \vec{ 0 } \) のとき \( \vec{ a } \ /\!/ \ \vec{ b } \ \Longleftrightarrow \ \vec{ b } = k \vec{ a } \) となる実数 \( k \) がある.
7 内積を用いたベクトルの直交条件(平行条件はクロス積を用いる) 8 内積の性質・公式. ここでは、 と が平行であるための条件をみてみましょう。 ではないベクトル、 があったときに、この2つのベクトルが平行であるためには次のどちらかの条件を満たしている必要があります。 となる実数「k」がある この2つの条件のうちどち. ベクトルの平行条件です。 平行の時は a ベクトル=k b ベクトル ですよね? なぜこの場合は K を使わないのですか.
5 内積とノルム(norm) 6 内積を用いたベクトルの交角の求め方;. は、元となったベクトル \(\vec{\ a\ },\vec{\ b\ }\) によって作られる 平行. ベクトルの平行条件の問題です。ベクトルは平行移動して重なるものは同じものとみなすので、3点が同一直線上にある条件も同義です。 1. (1) 2つのベクトル$\vec{a}=\left( \begin.
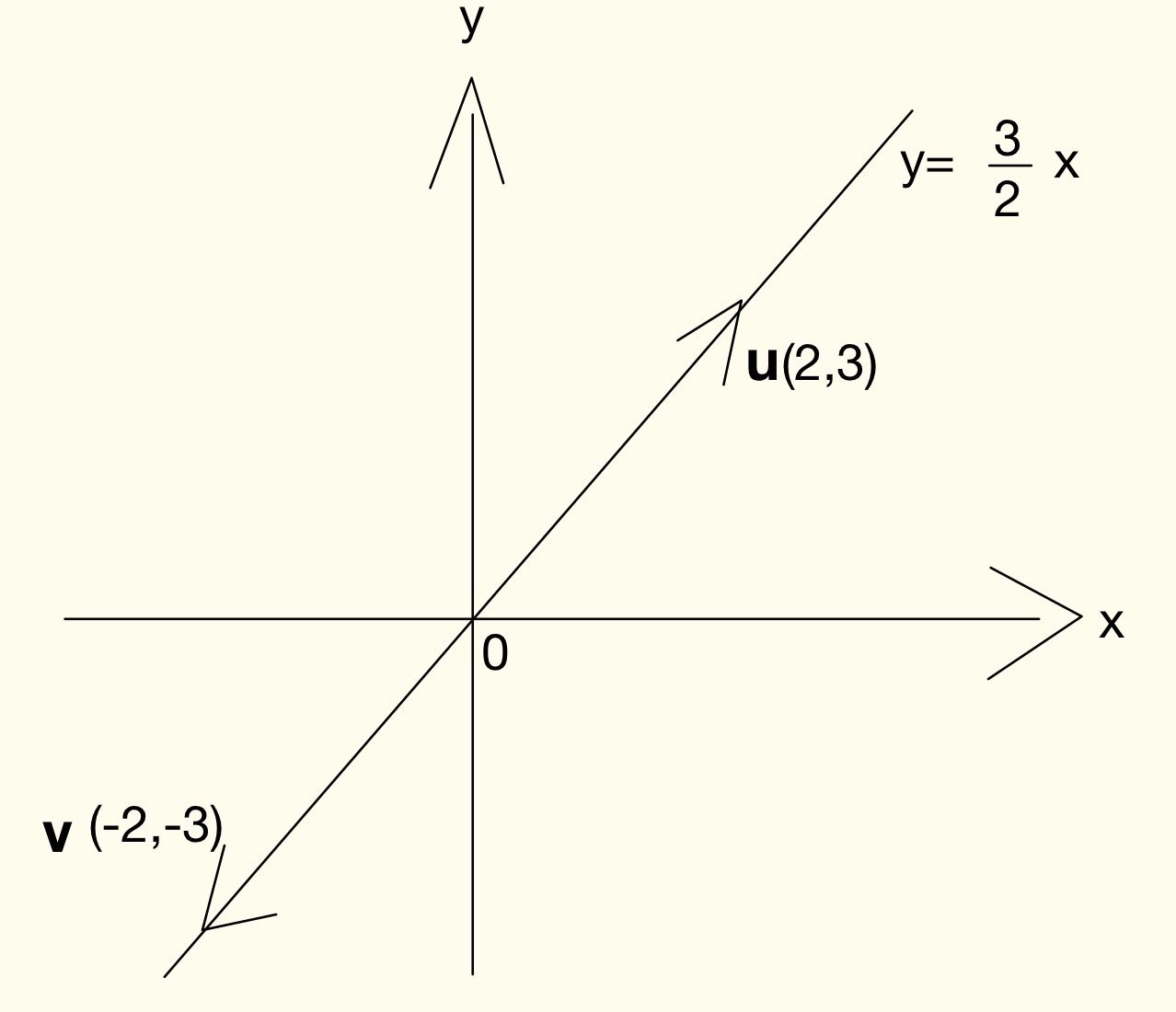
南海 まず でない二つのベクトル と が平行である条件から考えよう.. 史織 平行ということは方向が同じで大きさは違ってもよいということなので, 0でない実数 で. ベクトルの平行条件 \(\vec{0}\) でない 2 つのベクトル \(\vec{a}\), \(\vec{b}\) に対して、 \(\vec{a} \ // \ \vec{b} \iff \vec{a} = k \vec{b}\) となる実数 \(k\) がある.
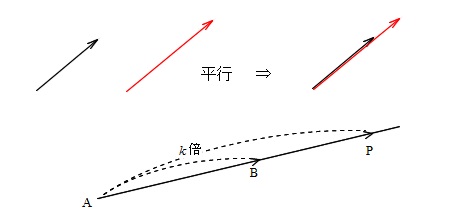
「2つのベクトルが平行になる」 元々ベクトルは方向性を持っています。 だから平行になるということは、 始点をそろえて、一方が他の実数倍になれば良い 、と言うことです。 3点\(\,\mathrm{A,B,P}\,\)が一直線上にあるという問題も、 始点を同じにすれば、. 2つのベクトルが1次独立なことの証明はそれほど難しくありません。 はじめに紹介した「 零ベクトルでない 」と「 平行でない 」を示せばokです。 前者は普通は明らかなので、大事なのは後者です。 前回、2つのベクトルが平行である条件を紹介しました。. 平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。(定義) 2 2組の向かいあう辺が、それぞれ等しい。(証明) 3 2組の向かいあう角が、それぞれ等しい。(証明).
ベクトルの平行条件については、以前にも学習しましたね。 あるベクトルcdが、別のベクトルabの実数k倍である とき、 ab//cd が成り立ちました。 その逆も真であり、 「ベクトルcdがベクトルabの実数倍」⇔「ベクトルabとベクトルcdは平行」 が成り立ちます。. つまり、2つのベクトルが平行の時は「 2つのベクトルの大きさをかけてあげるだけで内積が求まる 」ということです。 「平行」=「\(\overrightarrow{ a } \cdot \overrightarrow{ b }=|\overrightarrow{ a }||\overrightarrow{ b }|\)」と覚えてください! 2つのベクトルが垂直のときの内積. ここでは、 と が垂直であるための条件をみてみましょう。 ではないベクトル、 があったときに、この2つのベクトルが垂直であるためには次のどちらかの条件を満たしている必要があります。 この2つの条件のうちどちらか1つを満たしていれば.
CRC Hokkaido University X線の散乱 X線は電子より散乱される。 その散乱の強度は電子の密度に比例する。 散乱された波は互いに干渉するが、その 干渉の仕方は行路差による。 行路差は原点からの距離と波数とで とかける で干渉する。 k(=k2 −k1)•re−ik•r. ベクトルの問題の解答で aベクトル≠0,bベクトル≠0,aベクトルとbベクトルは平行ではないから…という言葉がありますが、これは何のために言っているのですか。 ベクトルaとベクトルbの始点を一致させるとV字ができると言いたいのです。始点を(0,0),aの終点を(1,0),bの終点を(0,1)である. 空間ベクトルで要となる問題ともいえる、同一平面上にある条件を求める問題を解説します。 ベクトルの成分を使った解き方と、平面の方程式を使ったとき方の両方を示しておきますので可能なら使って下さい。 空間図形を苦手にしているの ….
(別解1) …垂直条件を使って法線ベクトルを求める 点 を通り,2つのベクトル , で張られる平面と考える. 法線ベクトルを とおく により …(1) により …(2) 連立方程式(1)(2)は未知数が3個,方程式が2個なので,不定解を持つ.そこで1文字rについては解かないことにして,p,qをrで表す..

高校数学b 平行六面体と空間ベクトルの演算 受験の月

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

ゼロから理解するcgプログラミングのための数学 ベクトル編 Qiita
ベクトル 平行 条件 のギャラリー

ベクトルの平行条件は理解しているが このタイプの問題は解き 高校数学に関する質問 勉強質問サイト

高校数学b ベクトルの成分表示と平行四辺形 受験の月

高校数学b ベクトルの平行条件 練習編 映像授業のtry It トライイット

Aベクトルとbベクトルの 平行条件 垂直条件を教えて下さい Clear

高校数学b 四面体でのベクトルの表し方 映像授業のtry It トライイット

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

中3 2直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと

ベクトルの平行条件 ゼロからわかるベクトル第5回 Youtube

Aベクトルとbベクトルの 平行条件 垂直条件を教えて下さい Clear

高校数b ベクトル 30 10 ベクトルの平行条件 共線条件 勉強 Youtube スタディチューブ

高校数学b 平行条件と共線条件 映像授業のtry It トライイット

オンライン家庭教師 スナップアスク 本日の問題 今回はベクトルの平行条件です この公式 暗記で済ませていませんよね 高校数学 数学b 受験生 受験勉強 ベクトル

ベクトルの解析幾何学への応用1 円の接線の方程式 身勝手な主張
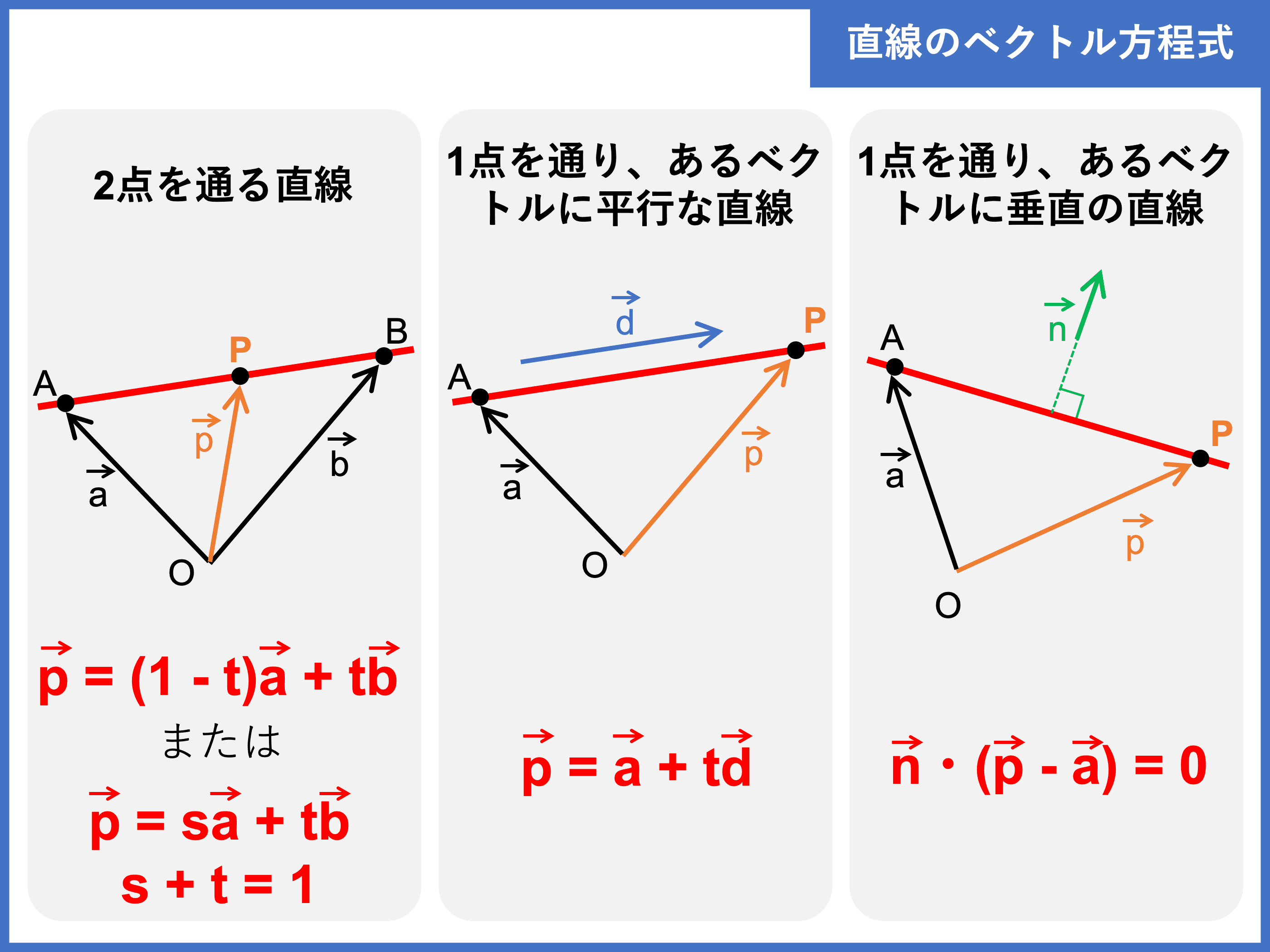
ベクトル方程式とは 図形別の公式 直線 円 法線など や問題の解き方をわかりやすく解説 受験辞典

ベクトルの解析幾何学への応用2 2直線の垂直条件 平行条件 身勝手な主張

平行条件と面積と行列式 怜悧玲瓏 高校数学を天空から俯瞰する

高校数学b 平行条件と共線条件 映像授業のtry It トライイット

高校数学b ベクトルの終点の存在範囲 受験の月

2つの直線が平行 垂直となる条件 数学の偏差値を上げて合格を目指す
ベクトルの平行条件で3点a B Cが同一直線上に存在する条件は Ab K A Yahoo 知恵袋

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ
Q Tbn 3aand9gcqs S1rona5weovtz3ght29i55dv6rq1bzo3y93mpuxbrraqecp Usqp Cau
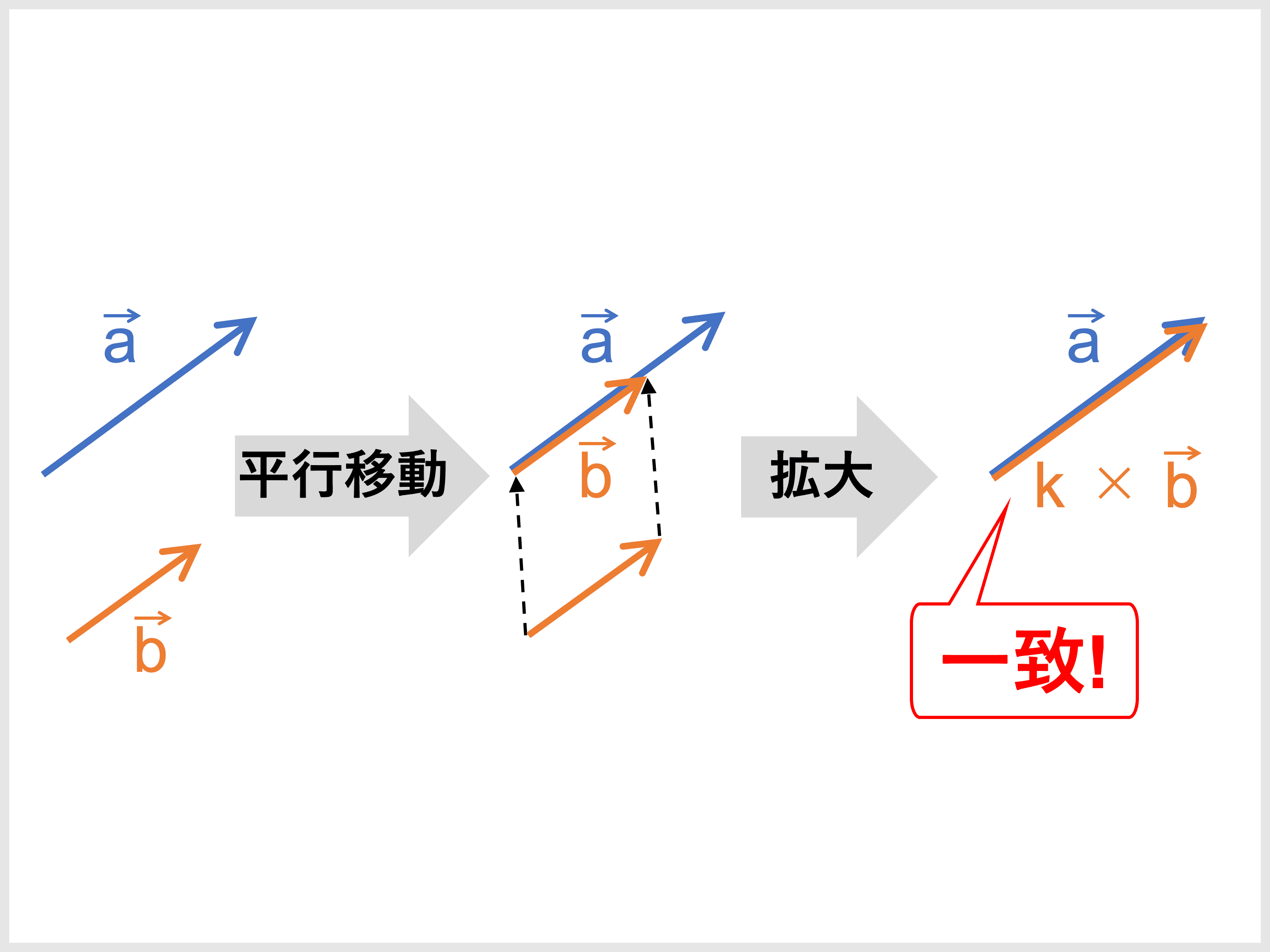
ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典

数学ii Bチェック リピート 第8章 1和と実数倍 3 平行条件 Pukiwiki

3分で分かる ベクトルの内積の2つの求め方 垂直 平行条件についてわかりやすく 合格サプリ

ベクトルの平行条件の所の問題です Clear
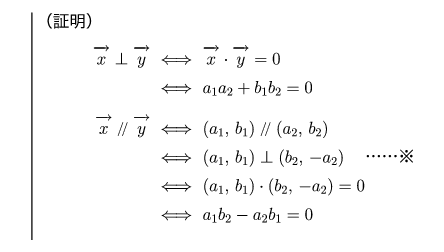
中3 2直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと

ベクトルの平行条件の所の問題です Clear

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

直線の方程式ax By C 0型の意味と垂直条件 平行条件 ラディカル高校数学

ベクトルの平行条件の所の問題です Clear

ゼロから理解するcgプログラミングのための数学 ベクトル編 Qiita

ベクトルの解析幾何学への応用1 円の接線の方程式 身勝手な主張

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ
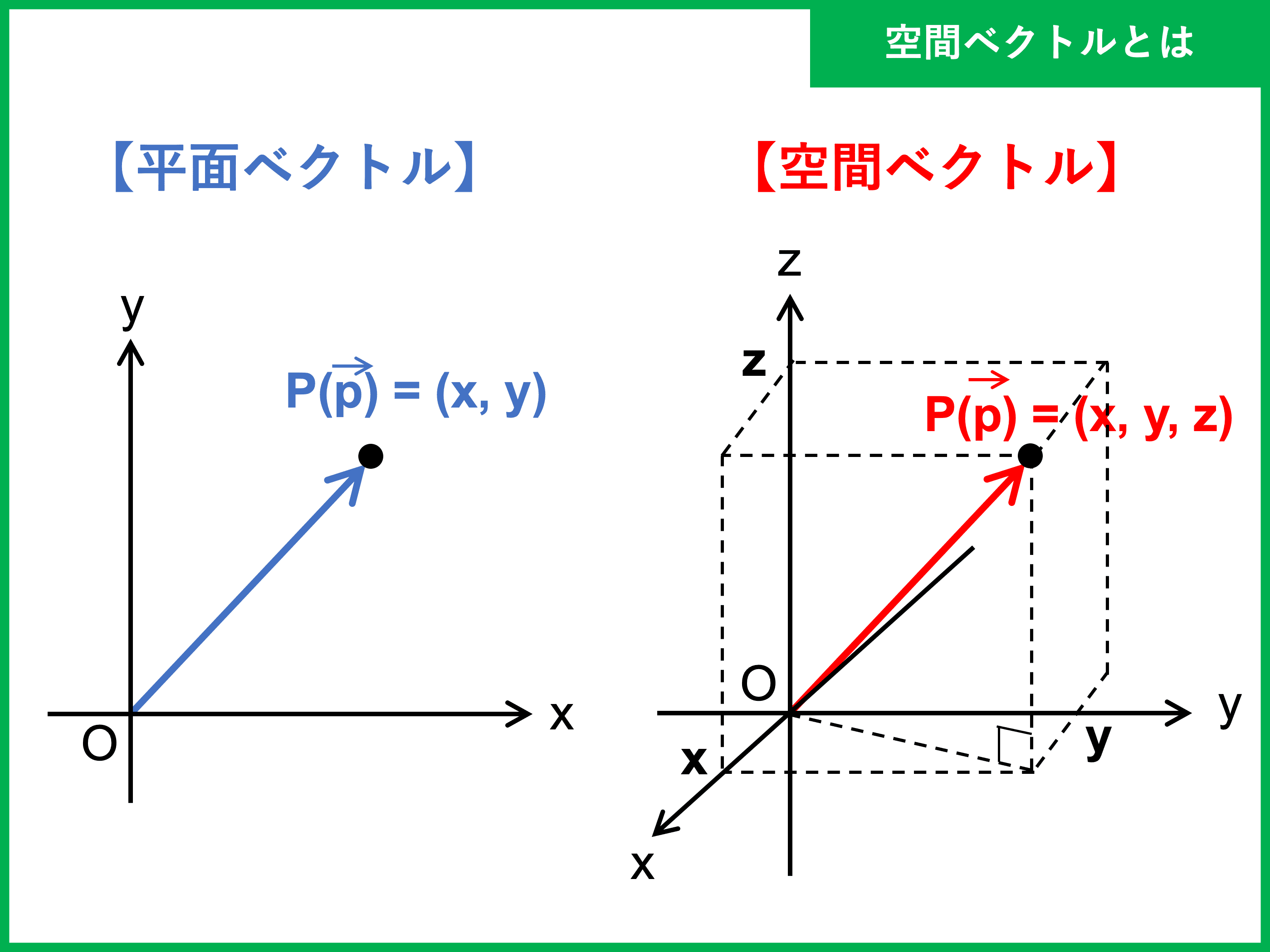
空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典
ベクトルの基本 平行と3点が一直線上にある条件

高校数学b ベクトルの内積とax Byの最大最小 受験の月

高校数学b 平行条件と共線条件 映像授業のtry It トライイット

ベクトルの平行条件は理解しているが このタイプの問題は解き 高校数学に関する質問 勉強質問サイト

数学b 平面ベクトル 解き方攻略ノート 高校生 数学のノート Clear
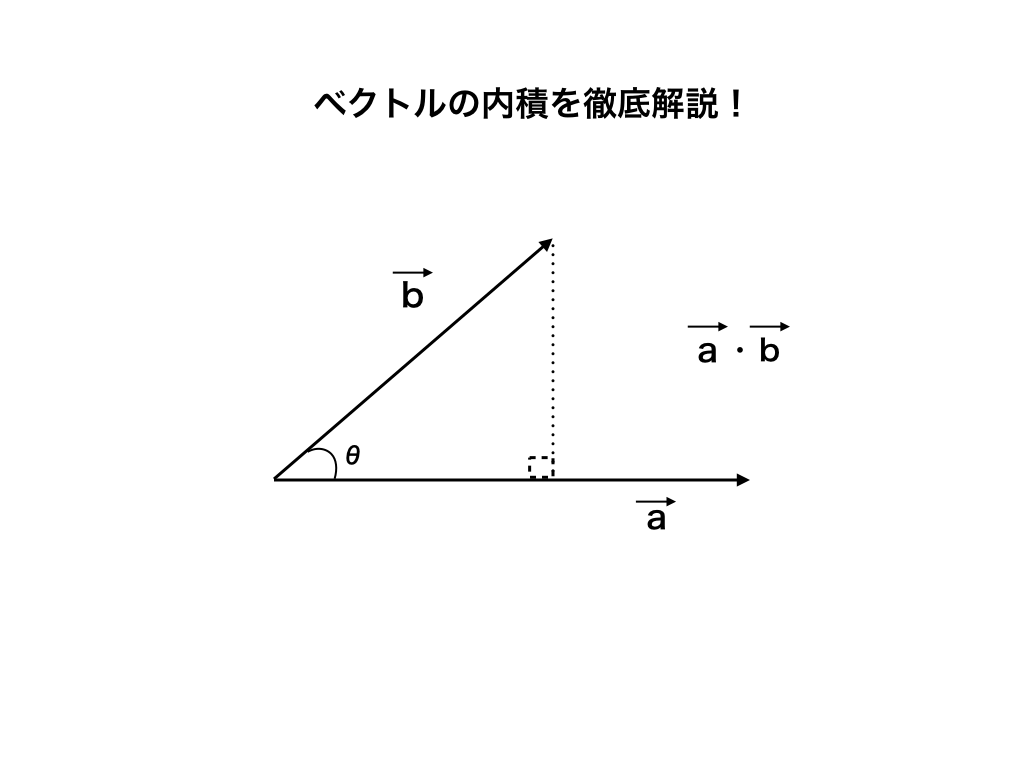
内積とは 定義と求め方 公式を解説 ベクトルの掛け算を分かりやすく

空間ベクトルの成分表示と垂直 平行条件をわかりやすく
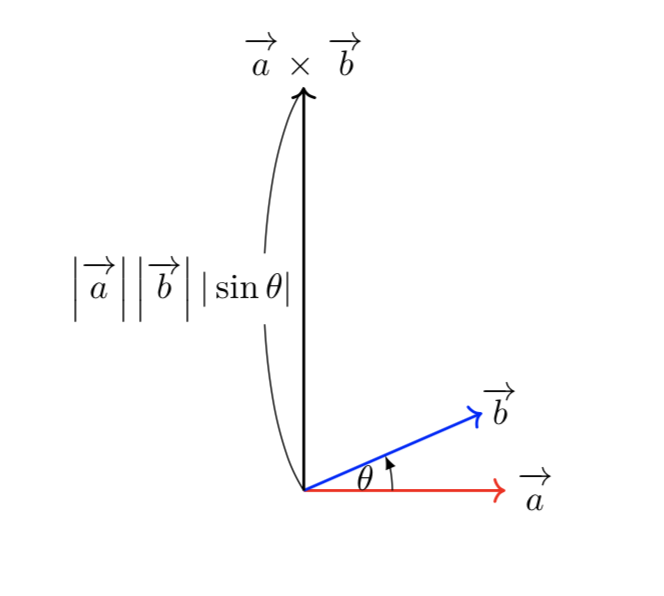
ベクトルの外積の公式やその覚え方とは 高校範囲で役立つ場面についても解説 東大医学部生の相談室

数学b 平面ベクトル 3 ベクトルの平行条件 高校生が数学のテストの前に見る授業 Youtube
数学bのベクトルの平行条件の問題なんですけど 合っていますか 間違えて Yahoo 知恵袋
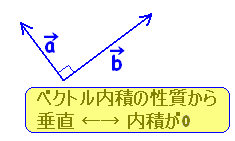
ベクトルの平行条件 垂直条件
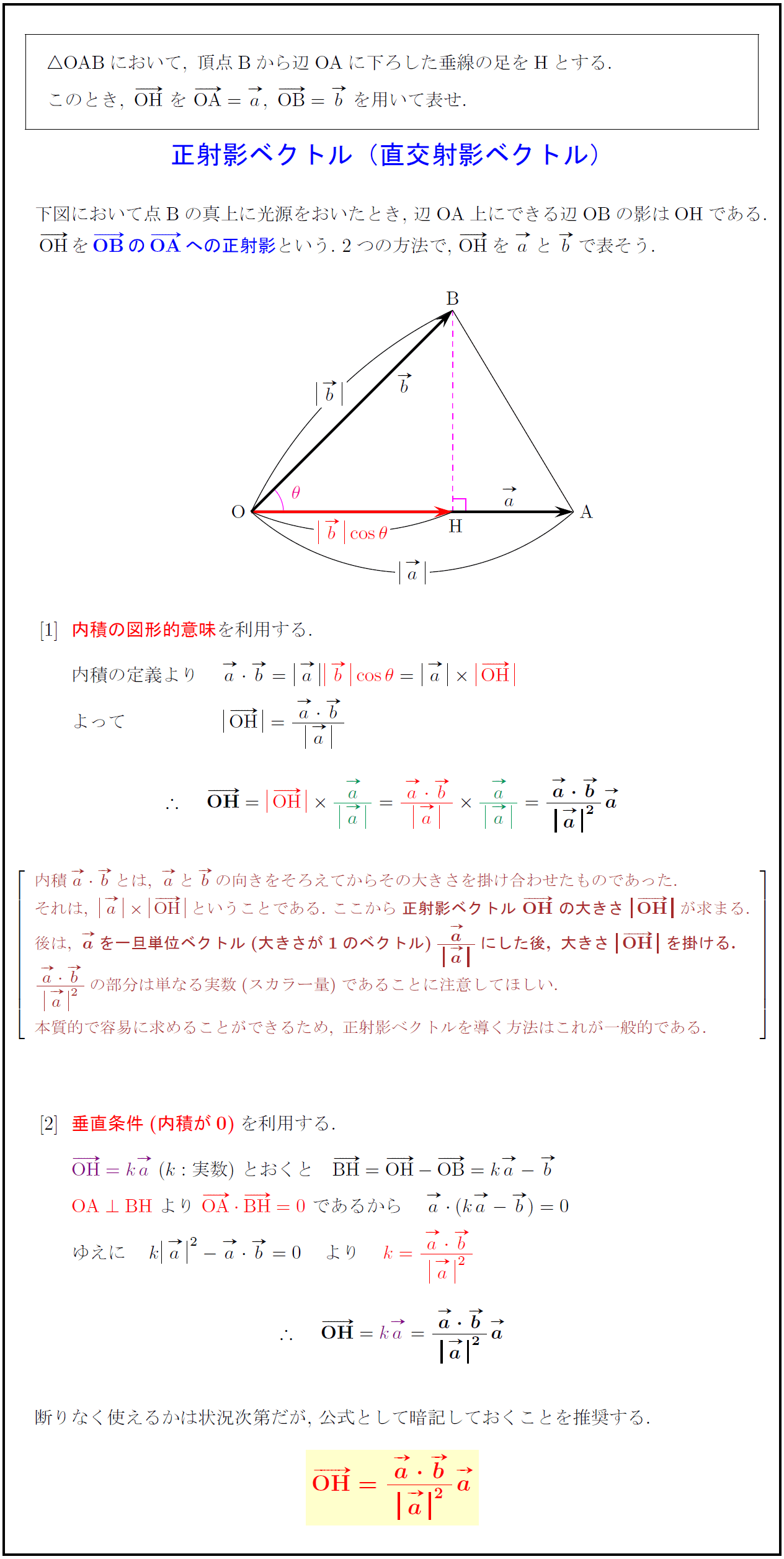
高校数学b 正射影ベクトル 直交射影ベクトル 受験の月

数学 ベクトル 平行条件 Youtube

ベクトルの平行条件 高校数学に関する質問 勉強質問サイト

ベクトルの平行条件 高校数学 ベクトル 7 Youtube

ベクトルの平行条件 Youtube
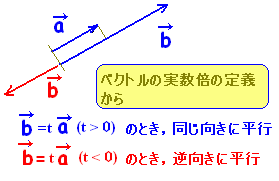
ベクトルの平行条件 垂直条件

ベクトルの演算 ベクトルの加法と減法 Ppt Download

数学b ベクトルの成分と平行条件の使い方とコツ 教科書より詳しい高校数学

平行と垂直 3 怜悧玲瓏 高校数学を天空から俯瞰する

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ
ベクトルの平行条件でaベクトル 0bベクトル 0と断るのはなぜですか 0ベ Yahoo 知恵袋

Aベクトルとbベクトルを反対にしたらダメですか 教えてください Clear
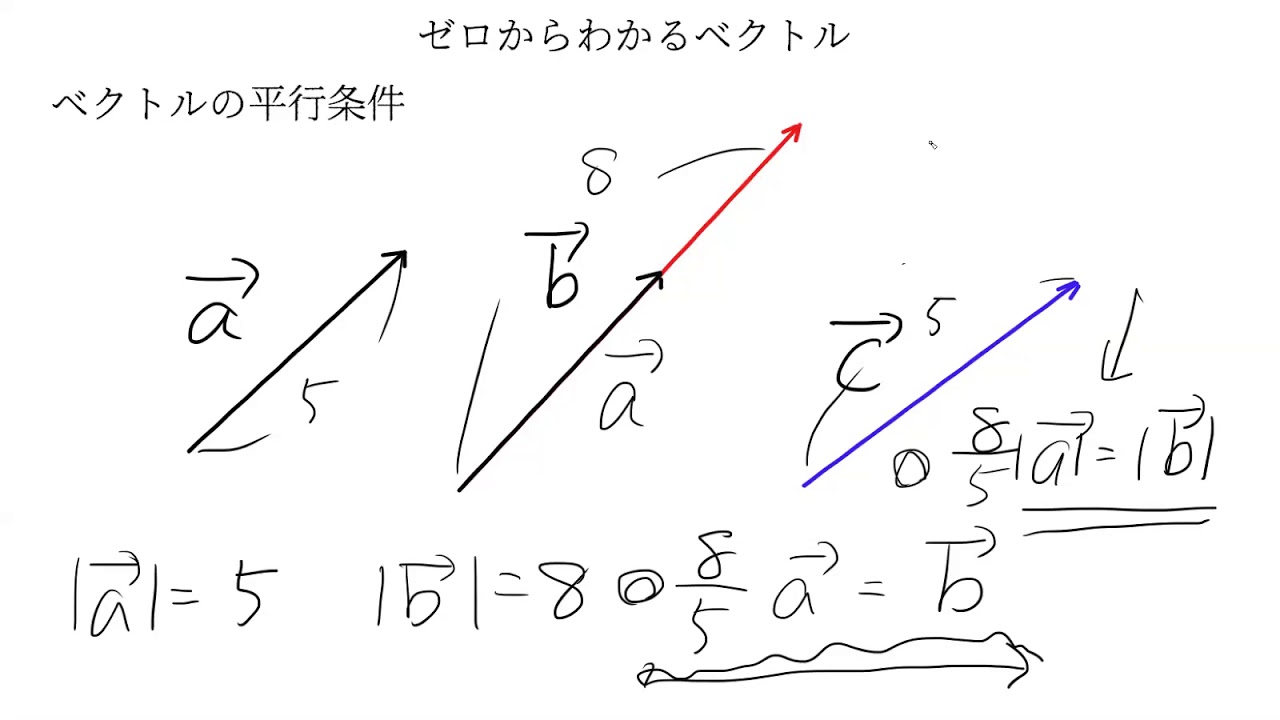
ベクトルの平行条件 ゼロからわかるベクトル第5回 Youtube
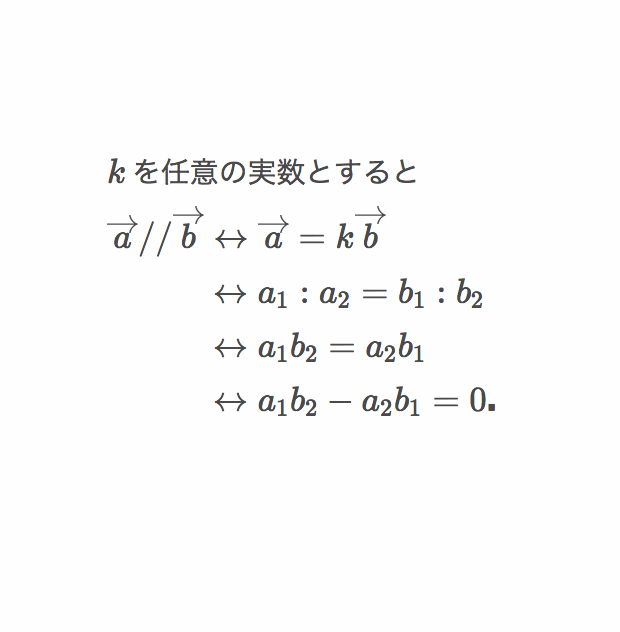
オンライン家庭教師 スナップアスク 本日の問題 今回はベクトルの平行条件です この公式 暗記で済ませていませんよね 高校数学 数学b 受験生 受験勉強 ベクトル

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ
様々な画像 ユニーク 垂直 ベクトル 求め 方

高校数学b ベクトルの共点条件 複数の点が一致する条件 受験の月
スローライフの森 数1 自家菜園 大人のさび落とし ベクトル003 ベクトルの実数倍

平行条件と面積と行列式 怜悧玲瓏 高校数学を天空から俯瞰する

下の問題なのですが 単位ベクトルの考え方が分からず 自分なり 高校数学に関する質問 勉強質問サイト

โน ตของ 数学b 2章 1節 平面上のベクトル ช น Senior Clear

基本 空間ベクトルの成分と平行 数b空間ベクトル2 09 Youtube

2 がわかりません 答え見てもわからないのですか やり方はこれしかないですか Clear
Q Tbn 3aand9gcqcuxk1alzi0ubb02m4edrdvqjyippcm0b1g56mulntfu5ihngm Usqp Cau

高校数b 平面ベクトル 平行条件 オンライン無料塾 ターンナップ Youtube

考え方はわかります 方向ベクトルがどうして 1 0 0 に 高校数学に関する質問 勉強質問サイト
中3 2直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと

ベクトルでは 恒等式のような考え方はできないのでしょうか 高校数学に関する質問 勉強質問サイト
ベクトルの平行条件についてです ベクトルの平行条件を使った問題で Yahoo 知恵袋

高校数学b 平行条件と共線条件 映像授業のtry It トライイット

高校数学 ベクトル 第6講 問3 ベクトルの平行条件の利用 標準レベル Youtube
平面ベクトルの平行条件についてです 画像の2 の2の最後の Yahoo 知恵袋

高校数学b ベクトルの平行条件 映像授業のtry It トライイット

高校 数学b ベクトル10 平行条件 13分 Youtube

ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ

高校数学b ベクトルの共線条件 3点が一直線上にある条件 受験の月

Studydoctorベクトルの垂直条件 数b Studydoctor

高校数学b ベクトルの平行条件 映像授業のtry It トライイット

高校数学 2直線の平行条件 垂直条件 一致条件とその証明 受験の月
W Cpq6sgizpgrm
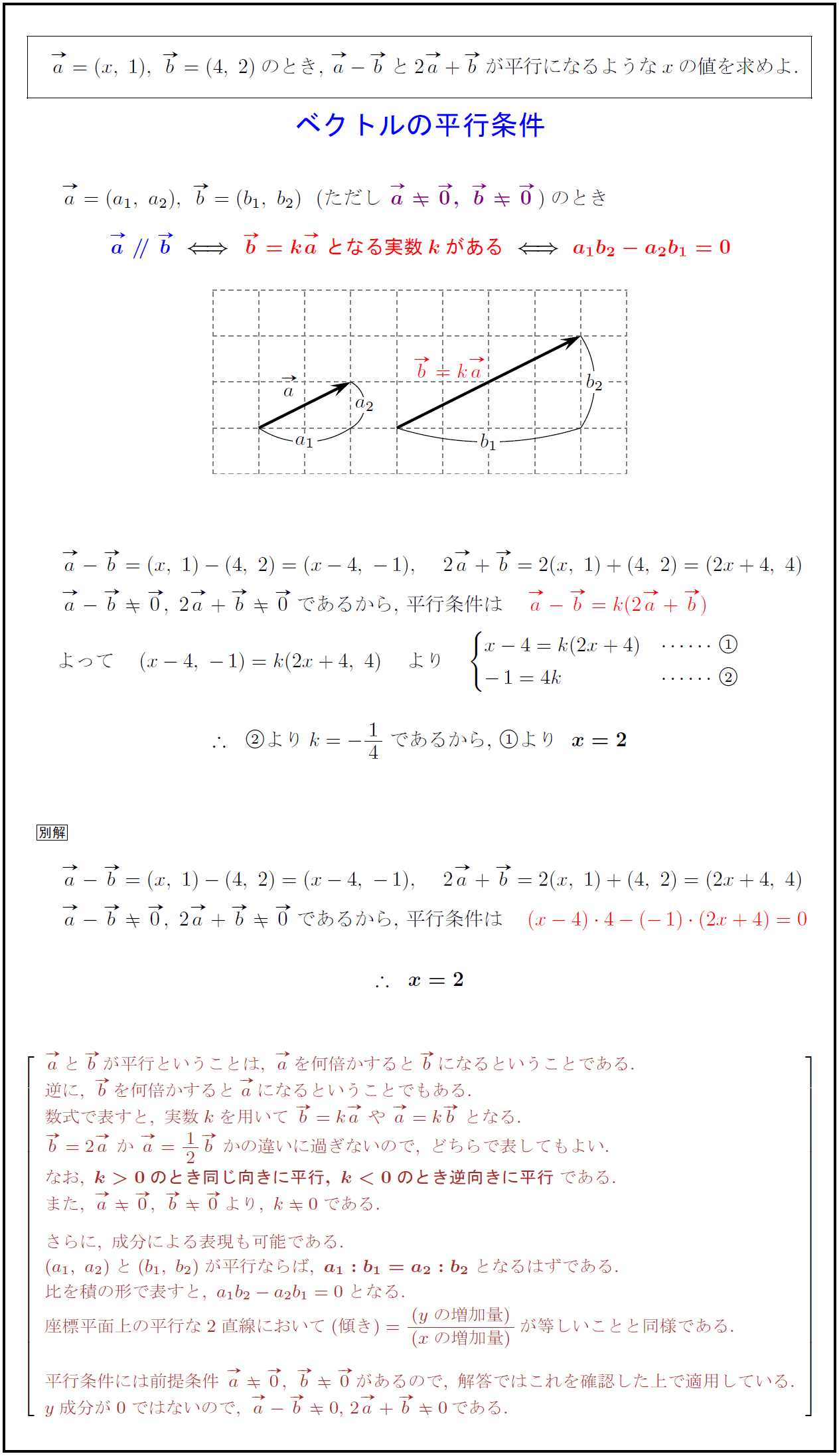
高校数学b ベクトルの成分表示と平行条件 受験の月

ベクトルとその演算 高校数学に関する質問 勉強質問サイト

下の問題なのですが 単位ベクトルの考え方が分からず 自分なり 高校数学に関する質問 勉強質問サイト

ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月

高校 数学b ベクトル10 平行条件 13分 Youtube

高校数学b ベクトルの垂直条件 映像授業のtry It トライイット

平行条件と面積と行列式 怜悧玲瓏 高校数学を天空から俯瞰する
2つのベクトルの平行条件と直角条件 受験初心者へ
ベクトルの平行条件 ベクトルの場合は 向きだけじゃなく大きさも等しくない Yahoo 知恵袋

ベクトルの平行条件 数学b フリー教材開発コミュニティ Ftext
Q Tbn 3aand9gctzwoirykxq0qtwhovoucfk6iupjhwic6rl0t4i Hp Ezk1arjo Usqp Cau

平行条件書かなきゃだめですか Clear
Q Tbn 3aand9gcrskk Rngyyrhinpjd9q3vhjdgrafdrnc8zpphhp U5sz1an2ug Usqp Cau

数学ii 平行条件と垂直条件 高校数学に関する質問 勉強質問サイト




